회전 행렬을 공부할 때 Euler angle, roll-pitch-yaw 와 같은 표현법에 대해서 공부한 적이 있다. 이번에는 이 전 글에서 배운 각속도를 이용해 회전 행렬의 또 다른 표현하는 방법에 대해서 공부해본다.

Vector Linear Differential Equation

이후 설명의 편의를 위해 선형 미분 방정식을 공부하고 가자. 대학교때 배우는 선형 미분 방정식과 다른점이 있다면 벡터 공간에서의 방정식을 푼다는 점이다.  문제 정의는 다음과 같다.

$$\dot{x}(t)=Ax(t) \\ \text{, where } x(t) \in \mathbb{R}^3, A \in \mathbb{R}^{3\times3}\text{ is constant}, x(0)\text{ is given}$$

해를 예측하고 확인해보는 방식을 이용한다. 해가 \(x(t)=e^{At}x(0)\) 이라고 가정해보자. 이 때 \(e^{At}\) 는 \(e^x=1+x+\frac{x^2}{2}…\)를 이용하여

$$ e^{At}=I+(At)+\frac{(At)^2}{2!}…$$

임을 알 수 있다. \(t\)는 상수 이므로

\(\begin{align} \dot{x}(t) &= (A + A^2t + \frac{A^3t^2}{2!}+…)x(0) \\ &= A(I+At+\frac{(At)^2}{2!}…)x(0) \\ &= Ae^{At}x(0) \\ &= Ax(t)\end{align}\)

이 되어서 최종적으로 위의 벡터 선형 미분 방정식의 해는

$$ x(t)=e^{At}x(0) $$

가 된다. 이제 \(e^{At}\)를 계산하는 방법에 대해서 알아보자. 두가지 경우로 나누어서 설명한다.

첫번째로 \(A\) 가 대각 행렬인 경우이다. \(A\)가 대각 행렬이면  

\(A = \left[\begin{array}{cccc} d_1 & 0 & 0 & \cdots \\ 0 & d_2 & 0 & \cdots \\ 0 & 0 & \ddots & \\ \vdots & \vdots & & d_n \end{array}\right]\)

로 쓸 수 있고 \(e^{At}\) 를 테일러 전개를 해서

\(\begin{align} e^{At} &= I+At+\frac{A^2t^2}{2!}+\frac{A^3t^3}{3!}+… \\ &= I + \left[\begin{array}{cccc} d_1 t & 0 & 0 & \cdots \\ 0 & d_2 t & 0 & \cdots \\ 0 & 0 & \ddots & \\ \vdots & \vdots & & d_n t \end{array}\right] + \left[\begin{array}{cccc} \frac{d^2_1 t^2}{2!} & 0 & 0 & \cdots \\ 0 & \frac{d^2_2 t^2}{2!} & 0 & \cdots \\ 0 & 0 & \ddots & \\ \vdots & \vdots & & \frac{d^2_n t^2}{2!} \end{array}\right] + … \\ &= \left[\begin{array}{cccc} 1 + d_1 t + \frac{d^2_1 t^2}{2!} & 0 & 0 & \cdots \\ 0 & 1 + d_2 t + \frac{d^2_2 t^2}{2!} & 0 & \cdots \\ 0 & 0 & \ddots & \\ \vdots & \vdots & & 1 + d_n t + \frac{d^2_n t^2}{2!} \end{array}\right] \\ &= \left[\begin{array}{cccc} e^{d_1 t} & 0 & 0 & \cdots \\ 0 & e^{d_2 t} & 0 & \cdots \\ 0 & 0 & \ddots & \\ \vdots & \vdots & & e^{d_n t} \end{array}\right] \end{align} \)

임을 알 수 있다.

두번째로 \(A\)가 대각 행렬이 아닌 경우이다. 선형 대수에서 배우는 고유값 분해 (eigendecomposition) 을 써서 어떤 대각 행렬 \(D\) 와 역행렬이 존재하는 \(P\)로 \(A\)를 표현 할 수 있다.

\(A = PDP^{-1}\)

그러면

\(\begin{align} e^{At} &= e^{(PDP^{-1})t} \\ &= I + (PDP^{-1})t + (PDP^{-1})(PDP^{-1})\frac{t^2}{2!} + … \\ &= I + PDP^{-1} + PD^2P^{-1}\frac{t^2}{2!} + … \\ &= P(I + Dt + D^2\frac{t^2}{2!}+…)P^{-1} \\ &= Pe^{Dt}P^{-1} \end{align}\)

이 됨을 알 수 있다. \(D\) 는 대각 행렬이므로 \(e^{Dt}\) 는 첫번째 경우를 이용하여 계산할 수 있다.

Exponential Coordinate of Rotations

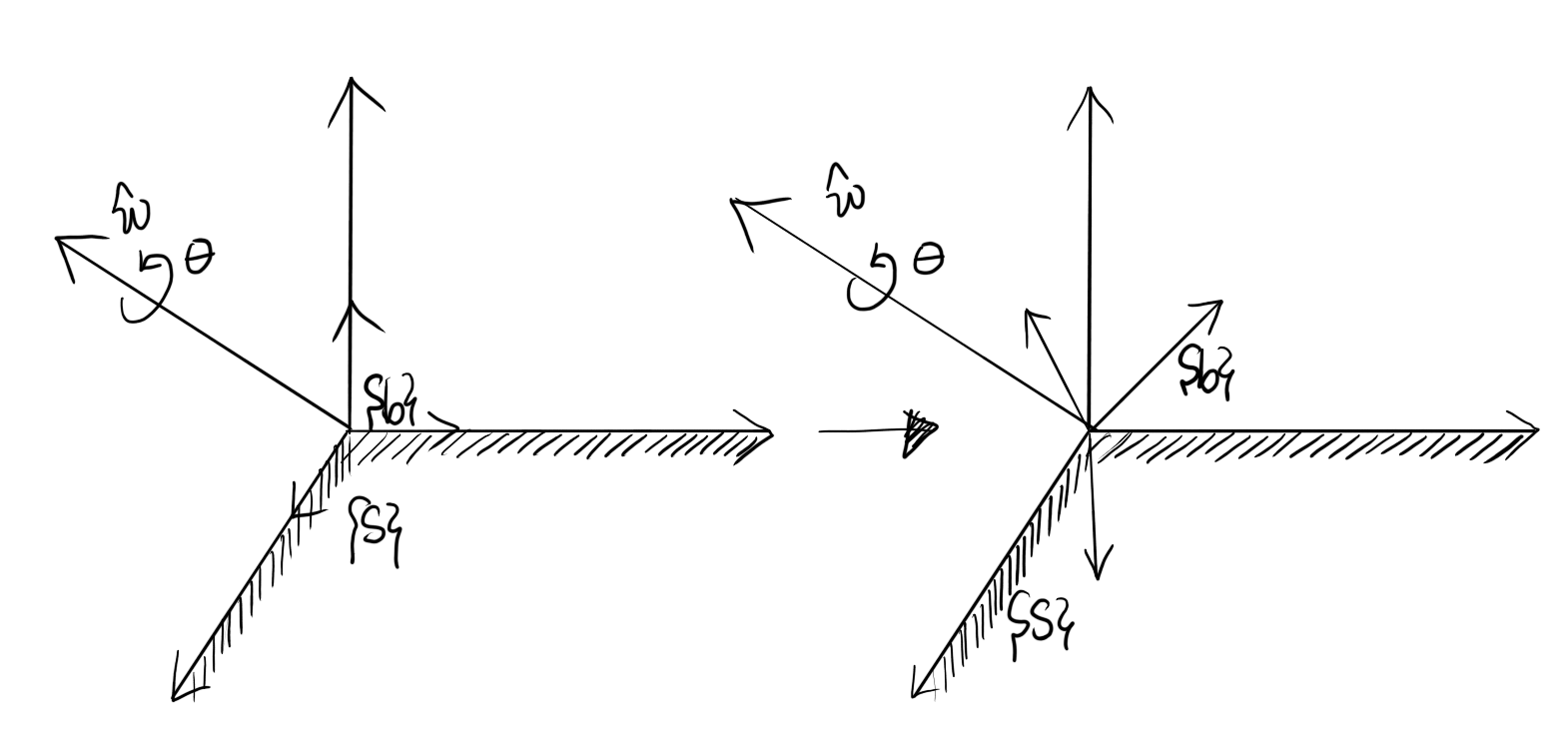
\(\vec{\omega}\) 을 기준으로 회전하는 frame \(\{b\}\) 와 고정된 frame \(\{s\}\) 가 있다. 시간 \(t\) 일 때 \(\vec{\omega}\) 를 frame \(\{s\}\) 에서 표현하면 좌표계와 회전축이 모두 고정되어 있으므로 시간이 관계없이 \(\omega_s\) 이고 frame \(\{s\}\) 에서 바라본 frame \(\{b\}\) 의 회전 행렬은 \(R(t)=R_{sb}(t)\) 이다. 이 때 \(\omega_s\) 와 \(R(t)\) 의 관계식은 이전 글에서 공부했듯이

\(\dot{R}=\left[\omega_s\right]R\)

이 된다. 이 미분방정식을 풀기 위해서 \(R(t)\) 를 아래처럼 쓰면 

\(R(t)=\left[\begin{array}{c|c|c} r_1(t) & r_2(t) & r_3(t) \end{array}\right]\)

각각의 열 \(r_i(t)\) 는 벡터 선형 미분 방정식

\(r_i(t) = \left[\omega_s\right]r_i(0)\)

으로 쓸 수 있고 이 때 해는 위에서 보았듯이

\(r_i(t)=e^{\left[\omega_s\right]}r_i(0)\)

이 된다. 이 결과를 모든 \(i = 1, 2, 3\)에 대해서 쓰고 정리하면

\(R(t)=e^{\left[\omega_s\right]}R(0)\)

이 됨을 알 수 있다. 만약에 회전하는 body frame 이 \(t = 0\) 일 때 fixed frame 과 같았다면 \(R(0)=I\) 이고 최종적으로 다음과 같은 결과를 얻을 수 있다.

$$ R(t)=e^{\left[\omega_s\right]t} $$

이제 식을 계산하기 편하도록 전개를 해볼텐데 그 전에 몇가지 생각해야 하는 것들이 있다.

우선 생각해봐야 하는 것은 \(\vec{\omega}\)와 \(\left[\omega_s\right]t\) 이다. \(\vec{\omega}\) 는 각속도 벡터를 의미한다. 이 말이 이해가 가지 않으면 전 포스트로 가서 \(\vec{\omega}\) 가 뭔지 다시 생각해자. 각속도 벡터 \(\vec{\omega}\) 를 frame \(\{s\}\) 에서 표현하면 \(\omega_s\) 이라고 했으므로 \(\omega_s=\hat{\omega}_s\|\omega_s\|\) 로 표현했을 때 \(\hat{\omega}_s\)와 \(\|\omega_s\|\) 는 각각 frame \(\{s\}\)에서 표현한 회전축 방향 (단위 벡터)와 각속력을 의미한다. 그러면 \(\left[\omega_s\right]t\) 는 \(\left[\hat{\omega}_s\|\omega_s\|\right]t\) 이 되고 \(\left[\cdot\right]\) 는 선형 mapping 이므로 \(\left[\hat{\omega}_s\right]\|\omega_s\|t\) 가 된다. \(\vec{\omega}\) 는 등각속도 이므로 \(\|\omega_s\|t\) 는 등가속력으로 시간 \(t\) 만큼 움직인 각도 \(\theta\)라고 쓸수있다. 결과적으로

\(\left[\omega_s\right]t = \left[\hat{\omega}_s\right]\theta\)

가 된다.

두번째는 screw-symmetric matrix \(\left[\omega\right]\) 이다. \(\left[\omega\right]\)의 특성방정식 \(P(s)\)을 구해보면

\(\begin{align} P(s) &= \text{det}\left(Is-\left[\begin{array}{ccc}0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{array}\right]\right) \\ &= s^3+(\omega_1^2 + \omega_2^2 + \omega_3^2)s \end{align}\)

이 된다. 만약에 행렬의 특성방정식을 모른다면 그냥 \(\text{det}\left(Is-\left[\omega\right]\right)\) 를 계산해도 괜찮다. 이 식에 \(\omega\) 가 단위 벡터라는 가정을 넣으면 \(\omega_1^2 + \omega_2^2 + \omega_3^2 = 1\) 이므로 \(P(s) = s^3 + s\) 가 된다. \(s\) 에 \(\left[\omega\right]\) 을 넣으면

\(P\left(\left[\omega\right]\right) = \left[\omega\right]^3 + \left[\omega\right]=0\)

이 되고 이를 정리하면

$$\left[\omega\right]^3 = -\left[\omega\right]$$

이라는 결과를 얻을 수 있다.

다시 돌아와 위의 사실을 생각하면서 \(R(t)\)를 테일러 전개를 하면

\(\begin{align} R(t) &= e^{\left[\omega_s\right]t} \\ &= I + \left[\omega_s\right]t + \left[\omega_s\right]^2\frac{t^2}{2!} + … \\ &= I + \left[\hat{\omega}_s\right]\theta + \left[\hat{\omega}_s\right]^2\frac{\theta^2}{2!} + … \\ &= I  + (\theta – \frac{\theta^3}{3!} + \frac{\theta^5}{5!} – …)\left[\hat{\omega}\right] + (\frac{\theta^2}{2!} – \frac{\theta^4}{4!} + …)\left[\hat{\omega}_s\right]^2 \\ &= I + \sin\theta \left[\hat{\omega}_s\right] + (1-\cos\theta)\left[\hat{\omega}_s\right]^2 \end{align}\)

이 된다. 정리하면, 처음 자세가 frame \(\{s\}\) 와 같은 frame \(\{b\}\) 를 \(\hat{\omega}\)축으로 \(\theta\) 만큼 돌렸을 때 frame \(\{b\}\)의 회전 행렬을 frame \(\{s\}\)에 대해서 표현하면

$$\begin{align} R &= e^{[\hat{\omega}]}\theta \\ &= I + \sin\theta \left[\hat{\omega}_s\right] + (1-\cos\theta)\left[\hat{\omega}_s\right]^2 \end{align}$$

이 된다. 이런식으로 exponential 을 이용해서 회전 행렬을 표현하는 방식을 exponential coordinate representation 이라고 한다.

Matrix Logarithm of Rotations

Exponential (지수)의 역은 로그이다. 위에서 exponential mapping 에 대해서 배웠으니 회전 행렬에 로그를 구해보는 시간을 갖도록 하자.

실수에 대해서 지수함수와 로그함수는

\(\exp: x\in\mathbb{R} \rightarrow e^x \in \mathbb{R}\)
\(\log: e^x \in \mathbb{R} \rightarrow x \in \mathbb{R}\)

인것처럼 회전 행렬에 대해서도 아래와 같이 쓸 수 있다.

\(\exp: \left[\hat{\omega}\right]\theta \in so(3) \rightarrow R=e^{[\hat{\omega}]} \in SO(3)\)
\(\log: R=e^{[\hat{\omega}]} \in SO(3) \rightarrow \left[\hat{\omega}\right]\theta \in so(3) \)

실제로 계산하는 방법은 

$$R = I + \sin\theta \left[\hat{\omega}_s\right] + (1-\cos\theta)\left[\hat{\omega}_s\right]^2 $$

을 이용하면 쉽게

$$\left[\hat{\omega}\right] = \frac{1}{2\sin\theta}(R-R^\text{T})$$

임을 보일 수 있다. 예외적으로 \(\theta = \pi, 2\pi …\) 인 경우 

\(\text{(i) } \theta = 0, 2\pi, 4\pi …: R=I\)
\(\text{(ii) } \theta = \pi, 3\pi, 5\pi …: \text{solve } R=e^{[\hat{\omega}]}\pi=I+2\left[\hat{\omega}\right]^2 \text{ for } \left[\hat{\omega}\right] \)

를 이용하면 회전 행렬의 로그값을 계산 할 수 있다.