얼마나 회전되어 있는지를 표현하는 rotation matrix, 얼마나 빠르게 회전 하는지를 표현하는 각속도 벡터 그리고 어떻게 회전하는지를 말하는 회전축, 이렇게 회전과 관련된 3가지 개념에 대해서 배웠다. 이러한 관계를 똑같이 rigid body motion 에서도 이야기 할 수 있다. Transformation matrix, twist 그리고 오늘 마지막으로 배울 screw가 있습니다.
“회전축 \(\hat{\omega}\) 를 기준으로 각속력 \(\dot{\theta}\) 로 움직일 때 각속도는 \(\hat{\omega}\dot{\theta}\) 이며 등각속도로 시간 \(t\) 가 지나면 처음 위치 (\(t=0\)) 일때를 기준으로 하여 \(e^{[\hat{\omega}]\theta}\) (여기서 \(\theta\) 는 \(\dot{\theta}t\)) 에 위치한다.”
“Screw \(S\) 를 기준으로 각속력 \(\dot{\theta}\) 로 움직일 때 twist 는 \(\mathcal{V}=S\dot{\theta}\) 이며 등각속도로 시간 \(t\) 가 지나면 처음 위치 (\(t=0\)) 일때를 기준으로 하여 \(e^{[S]\theta}\) (여기서 \(\theta\) 는 \(\dot{\theta}\)) 에 위치한다.”
Rigid-body motion 이 회전뿐만 아니라 이동까지 고려하고 있으므로 screw 는 회전축과 이동 방향 벡터에 대한 정보를 모두 담고 있다. 이번 시간에는 rigid-body motion 에서 가장 중요한 screw 에 대해서 공부한다.
Screw
Rigid body motion 에서 각속도와 속도를 표현하기 위해서 twist 를 이용했다. 각속도 \(\omega\)를 회전축 \(\hat{\omega}\) 을 기준으로 각속력 \(\dot{\theta}\) 로 움직인 것으로 표현할 수 있듯이 twist \(\mathcal{V}=\left(\begin{array}{c}\omega \\ v\end{array}\right)\) 도 마찬가지로 screw \(S\) 을 기준으로 각속도 \(\dot{\theta}\) 로 움직였다라고 생각할 수 있다. 즉, screw \(S\) 는 twist \(\mathcal{V}\) 를 \(\omega\) 로 normalize 한 것이다.
$$\mathcal{V}=S\dot{\theta}\text{, where } S=\left(\begin{array}{c}\hat{\omega} \\ \frac{v}{\|\omega\|}\end{array}\right), \|\hat{\omega}\| = 1,\dot{\theta}=\|\omega\|$$
(이제부터 각속도 벡터 또는 회전축을 표현할때 \(\hat{\omega}\) 뿐만 아니라 \(\omega\) 도 혼용해서 쓴다. 그러므로 수식에서 \(\omega\) 또는 \(v\) 가 나오면 그 상황에 맞게 해석한다.)
“Every rigid body motion can be expressed as a screw motion”
Chasles-Mozzi Theorem
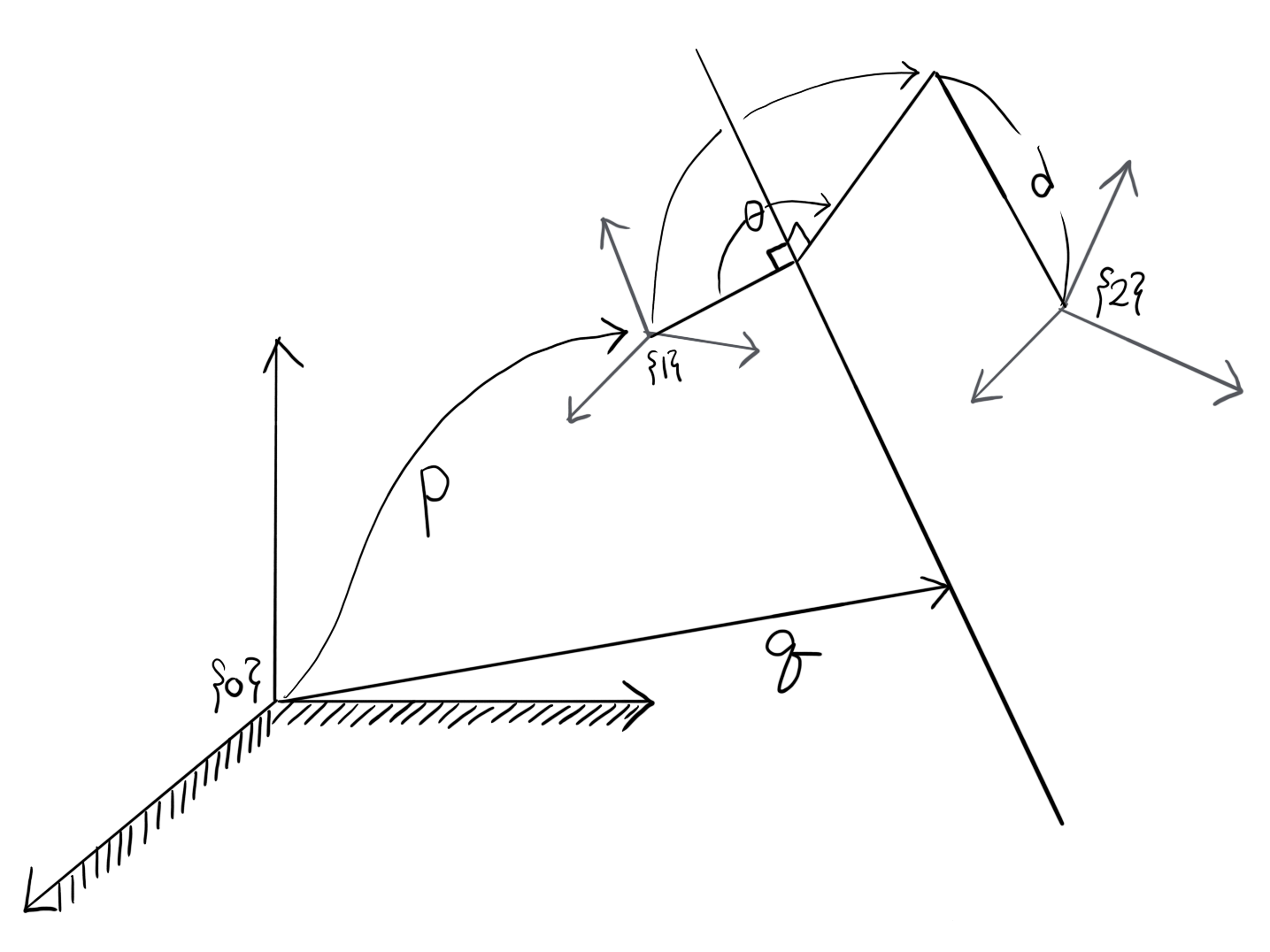
그림 1을 보자. 우리는 frame \(\{1\}\) 을 회전 및 이동을 시켜서 frame \(\{2\}\) 가 되게 하고 싶다. Chasles-Mozzi 이론은 이러한 rigid-body motion 이 screw motion 으로 표현 할 수 있음을 알려준다. Screw motion 이란 한국말로 나선 운동이라 하며, 어떤 회전축을 기준으로 회전하면서 회전축 방향으로 이동하는 움직임을 말한다. Screw motion 을 떠올릴때 회전과 동시에 회전축 방향으로 이동하는 것처럼 생각이 들지만 실제로는 순서대로 회전을 하고 그 다음에 이동을 해도 같은 결과를 얻는다.
다시 그림 1로 돌아와서 이야기를 이어가보자. Chasles-Mozzi 이론을 믿고 frame \(\{1\}\) 에서 frame \(\{2\}\) 로 움직이기 위한 회전축 하나를 잡는다. 그때 그 회전축은 \(q\) 를 지나며 방향은 \(\omega\) 이다. Frame \(\{1\}\) 과 frame \(\{2\}\) 를 frame \(\{0\}\) 을 기준으로 아래와 같이 표현하면
\(\begin{align} T_{01} &= \left[\begin{array}{cc}R & p \\ 0 & 1 \end{array}\right] \\ T_{02} &= \left[\begin{array}{cc}R^\prime & p^\prime \\ 0 & 1 \end{array}\right]\end{align}\)
\(R^\prime\) 과 \(p^\prime\) 은 다음과 같다.
\(\begin{align} R^\prime &= e^{[\omega]\theta}R \\ p^\prime &= q + e^{[\omega]\theta}(p-q)+\omega d\end{align}\)
여기서 \(\theta\) 는 회전축을 기준으로 회전한 각도를 이야기하며 \(d\) 는 회전축방향으로 이동한 거리를 말한다.
Definition
Screw pitch \(h\) is
$$h=\frac{d}{\theta}.$$
회전한 각도와 이동한 거리의 비를 screw pitch 라고 하고 위와 같이 정의한다.
Exponential Coordinate of Rigid-body Motions
Screw pitch 를 이용해서 \(T_{01}\) 과 \(T_{02}\) 의 관계식을 다시 써보면 아래와 같다.
\(\left[\begin{array}{cc}R^\prime & p^\prime \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} e^{[\omega]\theta} & \left(I – e^{[\omega]\theta}\right)q+h\theta\omega \\ 0 & 1 \end{array}\right] \left[\begin{array}{cc}R & p \\ 0 & 1 \end{array}\right]\)
두 transformation matrix 사이의 관계를 나타내는 행렬
\( \left[\begin{array}{cc} e^{[\omega]\theta} & \left(I – e^{[\omega]\theta}\right)q+h\theta\omega \\ 0 & 1 \end{array}\right] \)
를 screw \(S\) 를 이용해서 표현해보자.
Definition
\(S\) 가 \((\omega, v)\) 일때, \([S]\) 는 아래와 같이 정의한다.
$$\left[S\right] = \left[\begin{array}{cc} [\omega] & v \\ 0 & 0 \end{array}\right]\in\mathbb{R}^{4\times4}$$
그리고 우리는 \([S]\) 를 \(se(3)\) 라고 부르며 \(SE(3)\) 와 구분하기 위해 small 을 붙여서 말한다.
회전에 대해서 공부할 때, 회전축 \(\omega\) 으로 \(\theta\) 만큼 회전한 회전 행렬을 \(e^{[\omega]\theta}\) 로 표현했던 것처럼 rigid-body motion 에서도 비슷하게 \(e^{[S]\theta}\) 를 계산해보면 아래와 같다.
\(\begin{align} e^{[S]\theta} &= I + [S]\theta + [S]^2\frac{\theta ^2}{2!} + \cdots \\ &=\left[\begin{array}{cc} I + [\omega]\theta + [\omega]^2\frac{\theta^2}{2!} + \cdots & \left(I\theta + [\omega]\frac{\theta^2}{2!} + [\omega]^2\frac{\theta^3}{3!} + \cdots\right)v \\ 0 & 1 \end{array}\right] \\ &= \left[\begin{array}{cc} e^{[\omega]\theta} & G(\theta)v \\ 0 & 1 \end{array}\right] \end{align}\)
여기서 \(G(\theta)\) 는
\(G(\theta) = I\theta + (1-cos \theta)[\omega] + (\theta – sin \theta)[\omega]^2\)
이다. 그러면 \(e^{[S]\theta}\) 가 screw \(S\) 로 \(\theta\) 만큼 회전한 rigid-body motion 이 되도록 하는 \(v\) 를 찾기 위해서는 아래와 같은 식을 만족해야한다.
\(\left[\begin{array}{cc} e^{[\omega]\theta} & G(\theta)v \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} e^{[\omega]\theta} & \left(I-e^{[\omega]\theta}\right)q+h\omega \\ 0 & 1 \end{array}\right]\)
결론적으로 translation 파트만 같으면 된다.
\(G(\theta)v = \left(I-e^{[\omega]\theta}\right)q+h\omega \)
\(v\) 를 \(-\omega \times q + h \omega\) 라고 잡으면 위에 식이 성립하는 것을 확인 할 수 있다. (Hint: \(-\omega \times q = -[\omega]q\), \([\omega]\omega = 0\))
즉, \(q\)를 지나고 방향이 \(\omega\)인 축을 회전축으로 갖고 screw pitch가 \(h\)인 screw가 존재할 때 그 screw 를 기준으로 \(\theta\) 만큼 회전/이동하는 rigid-body motion은
\(T = e^{[S]\theta} \text{ where, } [S]=\left[\begin{array}{cc} \omega & v \\ 0 & 0 \end{array}\right] \in se(3)\)
이 되고 \(v\) 는 \(-\omega \times q + h \omega\) 가 된다.
Matrix Logarithm of Rigid-body Motions
\(T = \left[\begin{array}{cc} R & p \\ 0 & 1 \end{array}\right] \in SE(3) \rightarrow [S]\theta \in se(3)\)
회전 파트 \(R\) 을 이용해서 \(\omega\) 와 \(\theta\)를 구할 수 있다. \(\omega\) 와 \(\theta\) 를 이용하면 \(G(\theta)\)를 계산 할 수 있고 \(v\) 는 \(G^{-1}(\theta)p\)를 이용하면 쉽게 찾을 수 있다.