지금까지는 회전에 대해서만 공부했다. 이 글에서는 회전 (rotation)에 이동 (translation)을 모두 함께 다루는 표현에 대해서 공부해보자.
Homogeneous Transformation Matrices
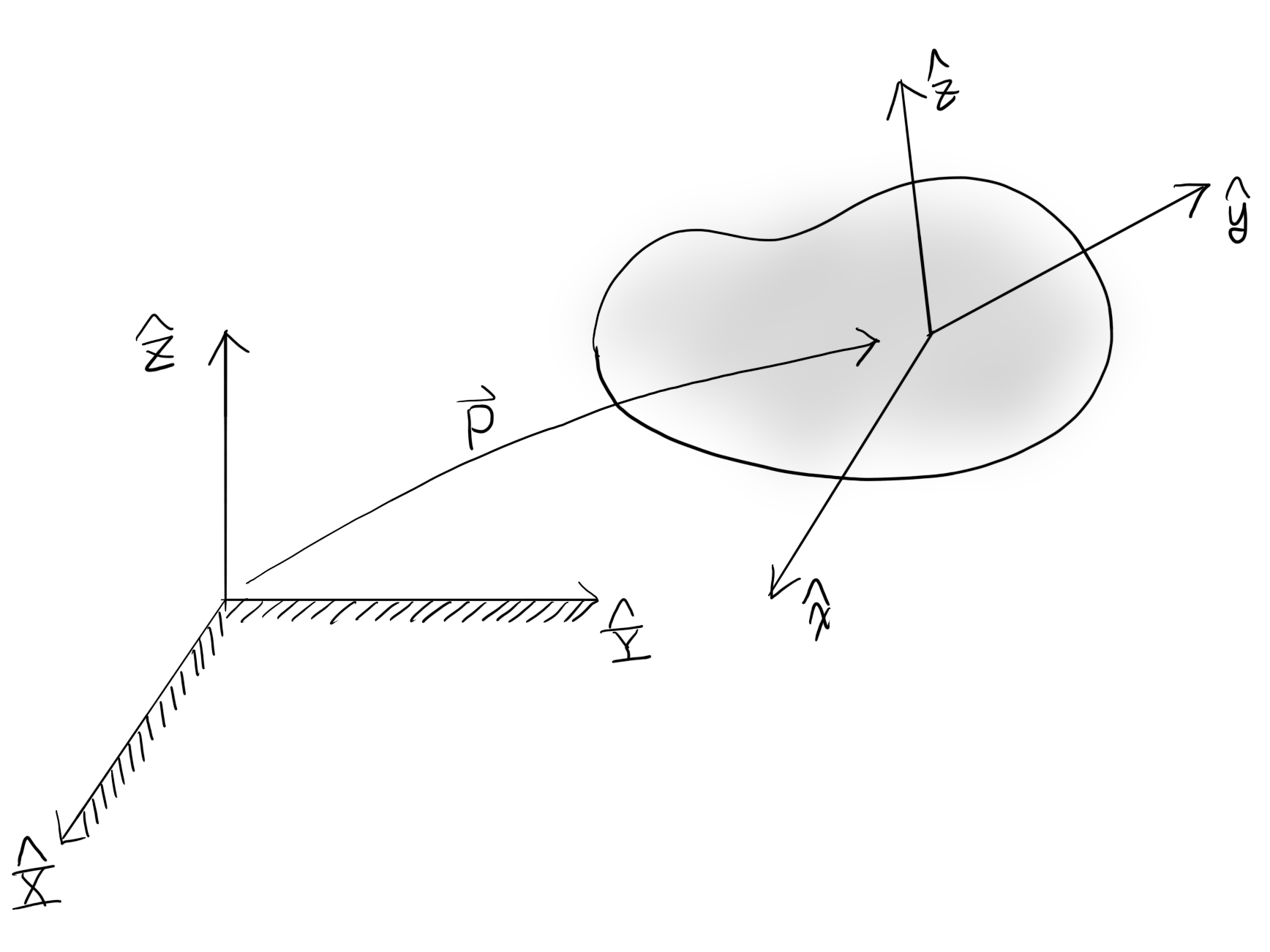
회전 행렬 공부했을때처럼 똑같이 body frame의 원점과 축들을 fixed frame을 기준으로 표현해보자.
\(\begin{align} \vec{P} &= p_1 \hat{X} + p_2 \hat{Y} + p_3 \hat{Z} \\ \hat{x} &= r_{11} \hat{X} + r_{21} \hat{Y} + r_{31} \hat{Z} \\ \hat{y} &= r_{12} \hat{X} + r_{22} \hat{Y} + r_{32} \hat{Z} \\ \hat{z} &= r_{13} \hat{X} + r_{23} \hat{Y} + r_{33} \hat{Z} \end{align}\)
회전 행렬 (rotation matrix) 를 아래와 같이 표현 했다면
\(R = \left[\begin{array}{ccc} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{array}\right]\)
이제 회전 정보와 함께 이동 정보도 함께 표현한 변환 행렬 (homogeneous transformation matrix)
\(T = \left[\begin{array}{ccc|c} r_{11} & r_{12} & r_{13} & p_1 \\ r_{21} & r_{22} & r_{23} & p_2 \\ r_{31} & r_{32} & r_{33} & p_3 \\ \hline 0 & 0 & 0 & 1 \end{array}\right] = \left[\begin{array}{cc} R & p \\ 0 & 1 \end{array}\right]\)
에 대해서 알아보자.
Definition
The Special Euclidean Group \(SE(3)\), also known as the group of rigid-body motions or homogeneous transformation matrices in \(\mathbb{R}^3\), is the set of all \(4\times4\) real matrices \(T\) of the form
$$ T=\left[\begin{array}{cc} R & p \\ 0 & 1 \end{array}\right] $$
where \(R \in SO(3)\), and \(p \in \mathbb{R}^3\) is a column vector.
정리하면 \(SE(3)\) 군 (group) 에 속하는 하나의 행렬 \(T\) 는 강체의 움직임을 표현하는 행렬로 해석할 수 있으며 \(R\) (rotation, 회전) 과 \(p\) (translation, 이동) 의 정보를 동시에 담고 있다. 여기서 짚고 넘어가야 할 부분이 있다. 바로 행렬 \(T\) 의 마지막 행 \(\left[\begin{array}{cccc} 0 & 0 & 0 & 1 \end{array}\right]\) 이다. Rotation 과 translation 과는 관련 없는 정보인거 같은데 왜 필요한 걸까?
Homogeneous Coordinates
다음 아래 그림을 보고 ①과 ②에 대해서 답해보자.

글씨가 잘 안보이는 분들을 위해 질문을 다시 쓰면
- 벡터 \(v\) 를 \(R\) 만큼 회전시키면?
- 벡터 \(v=v_b\) 를 \(\{s\}\) 에서 표현하면?
이다.
두 경우 모두 \(Rv\)가 된다. Rotation matrix 를 잘 이해하고 넘어왔다면 너무 쉽다. 만약에 \(Rv\)가 두 경우로 해석되는지 이해가 안가는 분들은 앞에가서 공부하고 오길 바란다. 자, 이제 아래의 그림을 보자.

마찬가지로 글씨가 잘 안보이는 분들을 위해 질문을 다시 적어주면
- 벡터 \(v\) 를 \(R\) 만큼 회전시키고 \(p\) 만큼 옮기면?
- Frame \(\{s\}\) 에서 표현한 frame \(\{b\}\) 의 원점과 자세는 각각 \(p=p_{sb}\) 그리고 \(R=R_{sb}\) 일때, frame \(\{b\}\) 에서 봤을 때 \(v\) 인 점을 frame \(\{s\}\) 에서 본다면?
이다.
공업 수업을 배웠다면 두 경우 모두 정답이 \(Rv+p\) 라는 것을 알 수 있다. 우리는 이 식을 linear transformation 즉, 행렬과 벡터의 곱의 형태로 바꾸고 싶다. 그렇게 하기 위해서 우리는 homogeneous coordinates 라는 개념을 가지고 온다. 동차좌표라는 뜻인데 정확한건 위키를 참고하고 우리는 차원을 하나 더 늘린 벡터라고 생각하자. 3차원 벡터 \(v\) 에 1을 추가한 벡터를 우리는 ‘\(v\)의 homogeneous coordinates 에서 표현’이라고 하고 다음과 같이 쓴다.
$$\left[\begin{array}{c} v \\ 1 \end{array}\right]$$
그러면 homogeneous coordinates 에서 표현한 \(v\)를 이용하여 위 그림에 대한 질문에 답을 해보자. (변환한 벡터도 똑같이 homogeneous coordinates 에서 표현한다.)
$$\left[\begin{array}{cc}R & p \\ 0 & 1\end{array}\right]\left[\begin{array}{c}v \\ 1 \end{array}\right] = \left[\begin{array}{c} Rv+p \\ 1 \end{array}\right] $$
앞에 곱해진 행렬을 보면 많이 본 식이 나온다. 바로 위에서 공부한 \(SE(3)\) 라는걸 확인 할 수 있다. 이처럼 homogeneous coordinates 에서 변환 행렬을 homogeneous transformation matrix 라고 부른다. 이로써 \(SE(3)\) 의 마지막 행이 왜 \(\left[\begin{array}{cccc} 0 & 0 & 0 & 1 \end{array}\right]\) 인지를 알 수 있었다.
다시 돌아가서 transformation matrix \(SE(3)\) 의 성질과 사용법에 대해서 공부해보자.
Properties of Transformation Matrix \(SE(3)\)
- \(T = \left[\begin{array}{cc} R & p \\ 0 & 1 \end{array}\right] \in SE(3)\) 는 역행렬을 갖는다. \(T^{-1} = \left[\begin{array}{cc} R^\text{T} & -R^\text{T}p \\ 0 & 1 \end{array}\right]\)
직접 \(TT^{-1}\) 과 \(T^{-1}T\) 를 계산해보면 쉽게 증명 할 수 있다.
- \(T_1, T_2, T_3 \in SE(3)\) 일때, 곱셈은 결합 법칙을 만족하지만 교환 법칙은 만족하지 않는다. \((T_1 T_2) T_3 = T_1 (T_2 T_3)\), \(T_1 T_2 \neq T_2 T_1\)
\(T_1, T_2, T_3\) 는 \(\mathbb{R}^{4\times4}\) 이므로 행렬의 성질을 모두 갖고 있으며 직접 곱셈을 해서 증명 해 볼 수 있다.
- \(T = (R, p) \in SE(3)\) 와 \(x, y \in \mathbb{R}^3\) 이 주어졌을 때, \(\|T_x – T_y\| = \|x-y\|\) 이다. 여기서 \(T_x\) 라는 의미는 벡터 \(x\) 를 \(R\) 만큼 회전시키고 \(p\) 만큼 이동했다는 의미를 갖는다.
이 성질은 두 벡터가 있을 때 각각의 벡터를 같은 transformation matrix 에 의해서 변환을 시켜도 두 벡터의 차는 항상 유지됨을 말해준다. 증명은 \(T_x\) 를 \(Rx+p\) 라고 두고 전개하면
\(\begin{align} \|(Rx+p) – (Ry+p)\| &= \|R(x-y)\| \\ &=\|x-y\| \end{align}\)
이 된다.
Use of Transformation Matrices \(SE(3)\)
- Frame 의 위치와 자세를 표현할때 사용함
우리가 앞에서도 공부했듯이 frame 의 위치와 자세를 표현할 때는 기준 frame이 존재 해야한다. 즉 아래 그림 [4]에서 frame \(\{b\}\) 의 위치와 자세를 frame \(\{a\}\) 기준으로 표현하면 \(T_{ab}=(R_{ab}, p_{ab})=\left[\begin{array}{cc} R_{ab} & p_{ab} \\ 0 & 1 \end{array}\right]\) 로 나타낼 수 있다.
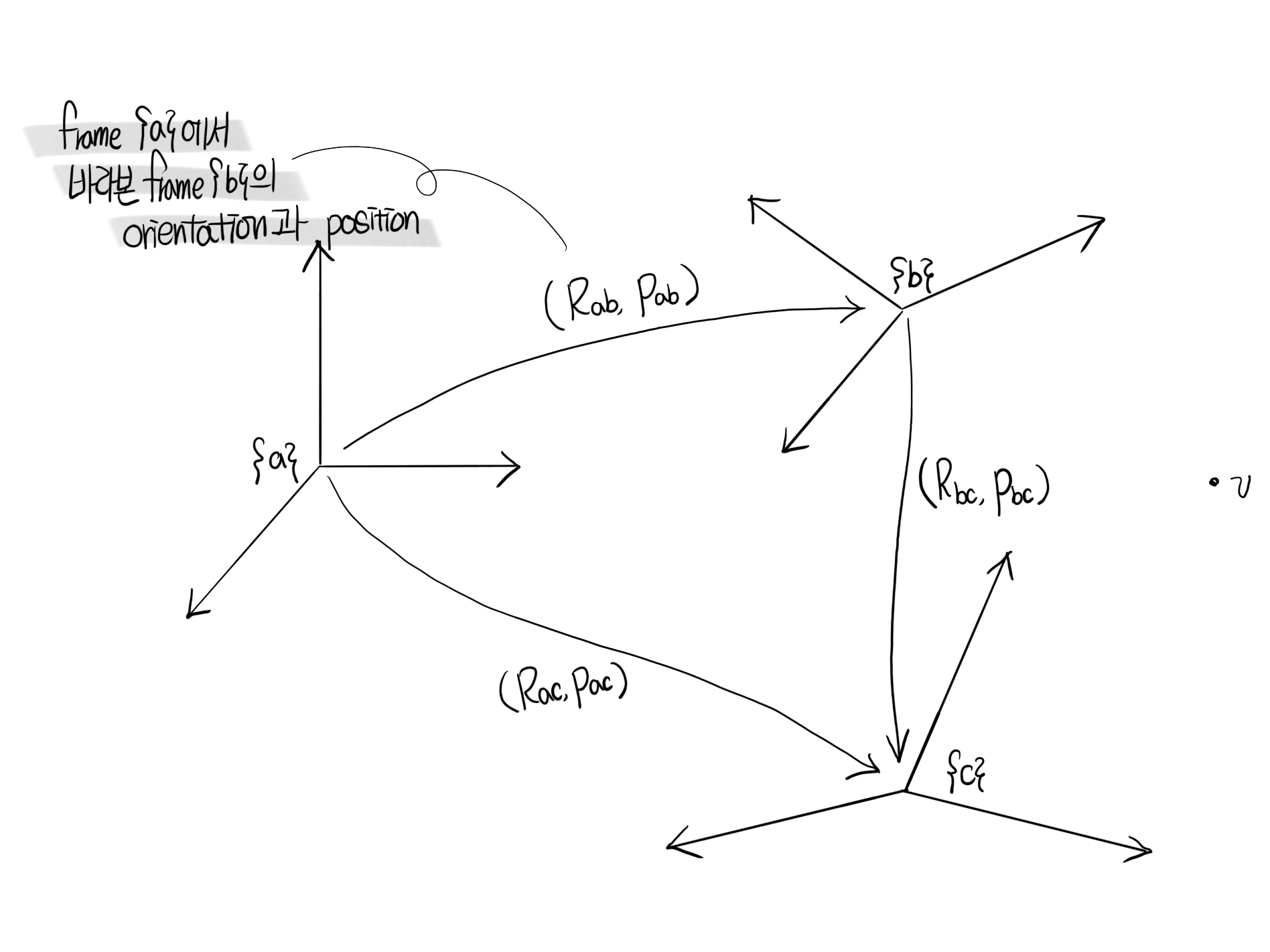
- 벡터와 frame 의 기준 frame 을 바꿀때 사용함
위 그림 [4]에서 frame \(\{c\}\) 를 frame \(\{b\}\) 에서 표현하면 \(T_{bc}\) 일 때 기준 frame 을 \(\{b\}\) 에서 \(\{a\}\) 로 바꾸고 싶다면
$$ T_{ac} = T_{ab}T_{bc} $$
처럼 하면 된다.
- 벡터와 frame을 회전 그리고 이동하고 싶을 때 사용함
벡터 \(v\)를 \(\hat{\omega}\) 를 기준으로 \(\theta\) 만큼 회전하고 \(p\) 만큼 이동하면
$$\text{Rot}(\hat{\omega},\theta) = \left[\begin{array}{cc} e^{[\hat{\omega}]\theta} & 0 \\ 0 & 1 \end{array}\right]$$
$$\text{Trans(p)}=\left[\begin{array}{cc} I & p \\ 0 & 1 \end{array}\right]$$
를 이용하여
$$\text{Trans}(p)\text{Rot}(\hat{\omega},\theta)v$$
해주면 된다. (\(v\) 에서 곱해지는 순서로 변환을 시켜준다라고 생각하면 된다. )
자, 다음 포스트로 넘어가기 전에 굉장히 중요한 이야기를 해보고 넘어갈까 한다.
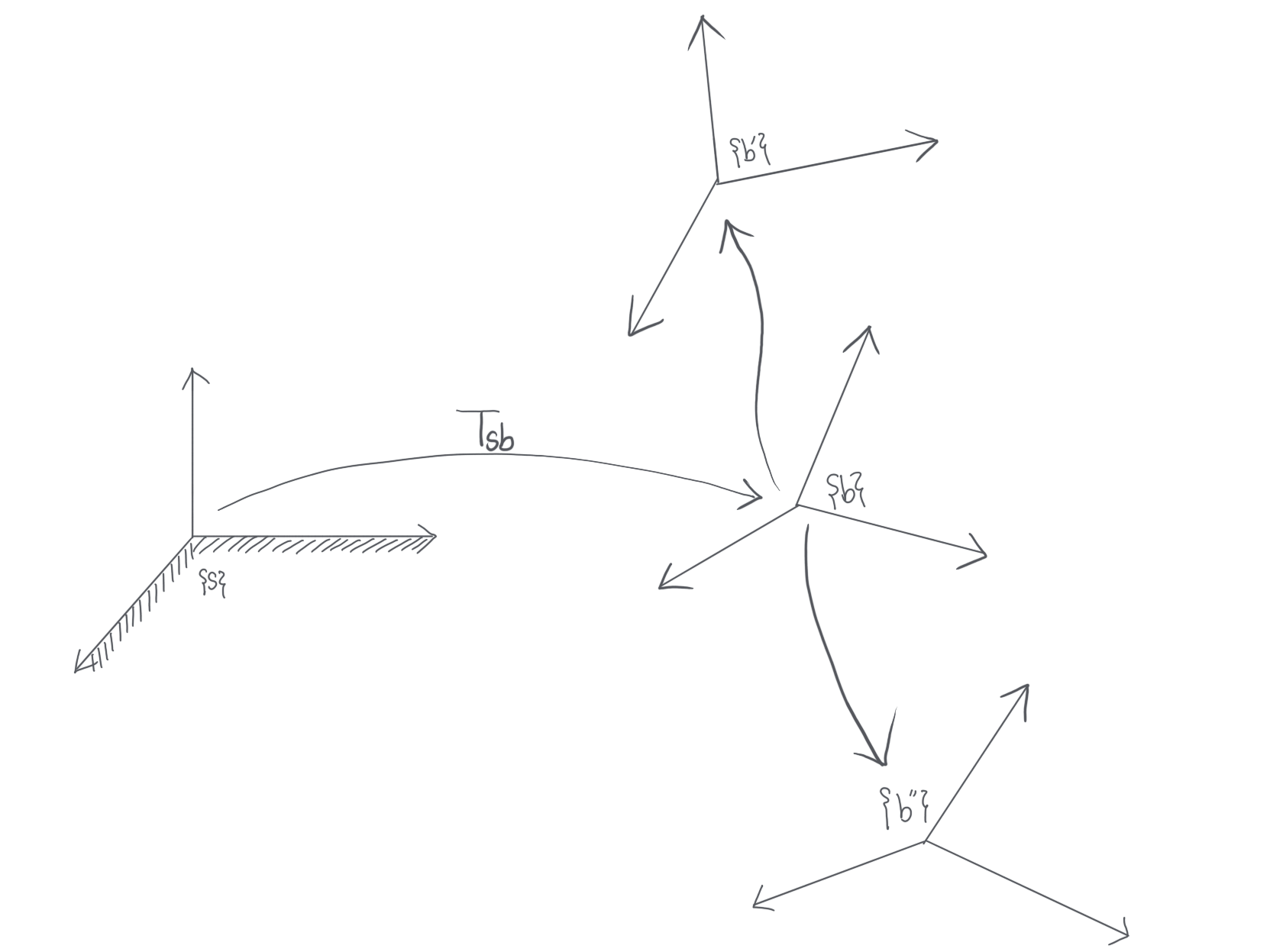
여기 두 frame \(\{s\}\)와 frame \(\{b\}\)가 있다. 그리고 frame \(\{b\}\)를 frame \(\{s\}\) 기준으로 표현했을 때 \(T_{sb}\) 이다. 변환 행렬 \(\text{Trans}(p)\) 와 \(\text{Rot}(\hat{\omega},\theta)\) 가 있을때 frame \(\{b\}\) 에 아래 식처럼 두개의 변환 행렬을 곱하려고 한다.
\(\begin{align}T_{sb^\prime}&=\text{Trans}(p)\text{Rot}(\hat{\omega},\theta)T_{sb} \\
T_{sb^{\prime\prime}} &= T_{sb}\text{Trans}(p)\text{Rot}(\hat{\omega},\theta)\end{align}\)
과연 frame \(\{b^\prime\}\) 과 \(\{b^{\prime\prime}\}\) 은 \(\{b\}\)에서 어떻게 움직였을까. 사실 해석하는 방법은 많이 있을 수 있지만 어떤 방식이든 수식 그대로 받아드리지 않고 식을 해석하고 풀어내야 나중에 복잡한 식이 나와도 쉽게 머릿속으로 frame 들을 움직여가면서 문제를 해결 할 수 있다. 다양한 해석 중에 하나를 공유한다.
먼저, 첫번째 식은 바로 전에 본 식이다. Frame \(\{b\}\) 를 \(\hat{\omega}\) 를 기준으로 \(\theta\) 만큼 회전하고 \(p\) 만큼 이동했을 때 얻을 수 있는 식이다. 여기서 중요한건 \(\hat{\omega}\) 와 \(p\) 는 고정 좌표계, 즉 frame \(\{s\}\) 를 기준으로 각각 회전축과 이동벡터를 표현한거라는 점이다.
두번째 식은 frame \(\{c\}\) 와 frame \(\{d\}\) 를 도입하여 해석 할 수 있다. Frame \(\{c\}\) 를 frame \(\{b\}\) 기준으로 \(T_{bc} = \text{Trans}(p)\) 위치한 곳에 설정하고 frame \(\{d\}\) 를 방금 결정된 frame \(\{c\}\) 기준으로 \(T_{cd} = \text{Rot}(\hat{\omega}, \theta)\) 위치한 곳에 둔다. 이때 frame \(\{d\}\) 를 frame \(\{s\}\) 기준으로 표현하면
\(\begin{align} T_{sd} &= T_{sb} T_{bc} T_{cd} \\ &= T_{sb} \text{Trans}(p) \text{Rot}(\hat{\omega}, \theta) \end{align}\)
으로 쓸 수 있으며 결과적으로 frame \(\{d\}\) 가 frame \(\{b^{\prime\prime}\}\) 이 됨을 알 수 있다. 여기서 중요한건 \(p\) 는 frame \(\{b\}\) 기준으로 이동한 벡터를 나타낸것이고 \(\hat{\omega}\) 는 frame \(\{c\}\) 기준으로 회전축을 나타냈다는 점이다. 다시 말하면 \(p\) 는 움직 좌표계 frame \(\{b\}\) 를 기준으로, \(\hat{\omega}\) 는 frame \(\{b\}\) 에서 표현 했을때 \(\text{Trans}(p)\) 에 위치한 frame 을 기준으로 변환식에 들어가는 값들을 나타냈다. 이는 움직 좌표계 frame \(\{b\}\) 가 변환 거듭해 나가면서 \(p\) 와 \(\hat{\omega}\) 를 표현했다고 해석 할 수 있다.
위에 두 식을 보면서 어떤 생각을 했는가, 하나는 고정 좌표계 frame \(\{s\}\) 를 기준으로 \(p\) 와 \(\hat{\omega}\) 를 얻었고 하나는 움직 좌표계 frame 기준으로 \(p\) 와 \(\hat{\omega}\) 를 얻었다. 이렇게 식으로 똑같이 \(\hat{\omega}\) 또는 \(p\) 라고 써놔도 기준이 되는 frame 이 다르기 때문에 전혀 다른 다른 변환을 이야기하고 있다는 점을 알아야한다.