지금까지는 표현하고자하는 body frame 은 움직이지 않았다. 지금부터는 body frame 이 시간에 따라서 움직이는 상황에 대해서 살펴볼 것이다.
Angular Velocity
시간에 따라서 움직이는 body frame 이 있을때 시간 \(t\) 에서 속도는 아래와 같이 쓸 수 있다.
\(\begin{align}\dot{\vec{P}}
(t) &= \left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z}\end{array}\right]\left[\begin{array}{c}\dot{P}_x (t) \\ \dot{P}_y (t) \\ \dot{P}_z (t) \end{array}\right] \\ \left[\begin{array}{ccc}\dot{\hat{x}}(t) & \dot{\hat{y}}(t) & \dot{\hat{z}}(t)\end{array}\right] &= \left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z} \end{array}\right]\dot{R}(t)\quad— (1) \end{align}\)
우리는 지금 회전만을 다루고 있으므로 \(\dot{R}\) 을 좀 더 자세하게 살펴보자.
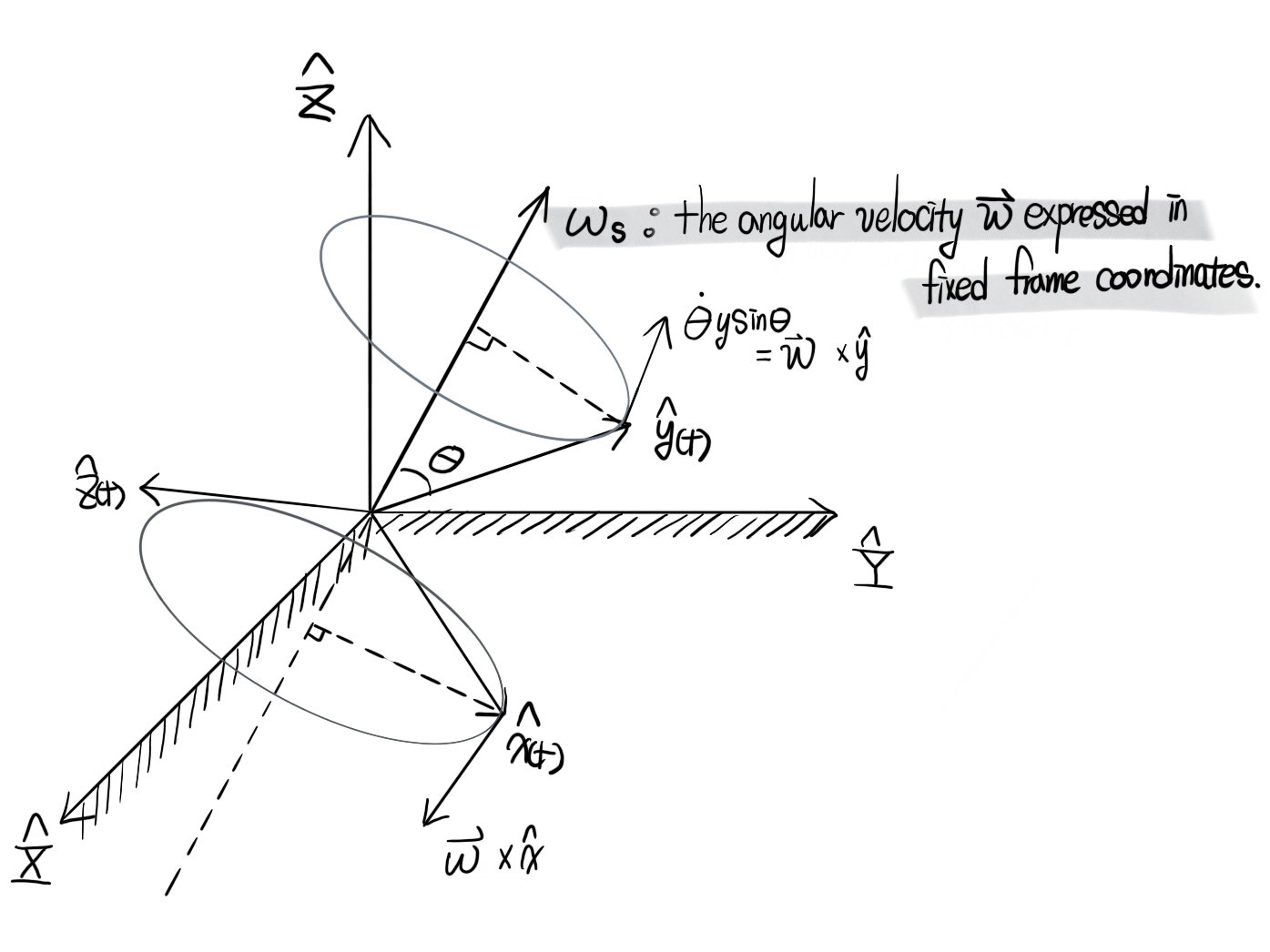
\(\left(\hat{x}(t), \hat{y}(t), \hat{z}(t)\right)\) 을 축으로 갖는 frame 이 \(\vec{\omega}\) 를 기준으로 회전하고 있다. 여기서 \(\omega_s\)는 fixed frame 에서 표현한 \(\vec{\omega}\) 이다.
$$\vec{\omega}=\left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z}\end{array}\right]\omega_s = \left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z}\end{array}\right]\left[\begin{array}{c} \omega_{s, x} \\ \omega_{s, y} \\ \omega_{s,z} \end{array}\right]\quad— (2)$$
\(\hat{x}(t), \hat{y}(t), \hat{z}(t)\) 을 축으로 보지말고 vector 라고 생각하면 \(\vec{\omega}\)로 회전하는 vector 의 속도는
\(\begin{align}
\dot{\hat{x}} &= \vec{\omega}\times\hat{x} \\
\dot{\hat{y}} &= \vec{\omega}\times\hat{y} \\
\dot{\hat{z}} &= \vec{\omega}\times\hat{z} \end{align}\)
이 된다. 이를 정리하면
$$\begin{align}\left[\begin{array}{ccc} \dot{\hat{x}} & \dot{\hat{y}} & \dot{\hat{z}} \end{array}\right] &= \left[\begin{array}{c|c|c} \vec{\omega}\times\hat{x} & \vec{\omega}\times\hat{y} & \vec{\omega}\times\hat{z} \end{array}\right] \\ &= \vec{\omega}\times\left[\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \end{array}\right] \quad— (3) \end{align} $$
이 됨을 알 수 있다. 여기서 \(\vec{\omega}\) 와 \(\hat{x}, \hat{y}, \hat{z}\) 를 fixed frame 에서 표현한 3차원 vector 라고 생각하면 위의 식을 아래처럼 쓸 수 있다.
$$\left[\begin{array}{ccc} \dot{\hat{x}} & \dot{\hat{y}} & \dot{\hat{z}} \end{array}\right] = \left[\omega_s\right] \left[\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \end{array}\right]$$
\(\left[\omega_s\right]\) 가 처음 등장하는데 우리는 이를 \(\omega_s\) 의 \(3\times3\) screw-symmetric matrix 라고 부른다.
Definition
Given a vector \(x=(x_1, x_2, x_3)\in \mathbb{R}^3\), define
$$\left[x\right]=\left[\begin{array}{ccc}0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{array}\right]. $$
The matrix \(\left[x\right]\) is a \(3\times3\) screw-symmetric matrix representation of x; that is \(\left[x\right]=-\left[x\right]^\text{T}\). The set of all \(3\times3\) skew-symmetric matrix is called \(so(3)\) which is the Lie algebra of \(SO(3)\).
위 정의는 지금까지 우리가 해왔던 외적을 행렬 형태로 표현 할 수 있고 그 행렬을 \(3\times3\) screw-symmetric matrix 라고 부르며 \(SO(3)\)의 Lie algebra, \(so(3)\), 라는 것을 말해준다.
Proposition
- Given any \(\omega \in \mathbb{R}^3\) and \(R \in SO(3)\), the following always holds:
$$R\left[\omega\right]R^\text{T} = \left[R\omega\right].\quad— (4)$$
- Given \(a, b, c \in \mathbb{R}^3\), if \(a \times b = c\), then
$$\left[a\right]\left[b\right]-\left[b\right]\left[a\right]=\left[c\right].$$
이제 위의 식들을 이용해서 \(\omega_s\)와 \(R\) 의 관계식을 구해보자. 식을 전개하기 전에 \(\left[\begin{array}{ccc} \hat{X} & \hat{Y} & \hat{Z} \end{array}\right]\) 은 \(SO(3)\) 의 조건을 모두 만족하므로 \(SO(3)\) 에 속한다는 사실을 기억하자.
식 (2)를 식 (3)에 넣고 식 (4)를 적용하면
$$\vec{\omega}\times \left[\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \end{array}\right] =
\left[\begin{array}{ccc} \hat{X} & \hat{Y} & \hat{Z} \end{array}\right] \left[\omega_s\right]
\left[\begin{array}{ccc} \hat{X} & \hat{Y} & \hat{Z} \end{array}\right]^\text{T}
\left[\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \end{array}\right] $$
이 된다. 여기서 \(\left[\begin{array}{ccc} \hat{x} & \hat{y} & \hat{z} \end{array}\right]\) 가 \(\left[\begin{array}{ccc} \hat{X} & \hat{Y} & \hat{Z} \end{array}\right]R\) 이라는 사실을 적용하여 식 (1)과 함께 쓰면 아래와 같다.
$$\begin{align} \left[\begin{array}{ccc}\dot{\hat{x}}(t) & \dot{\hat{y}}(t) & \dot{\hat{z}}(t)\end{array}\right] &= \left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z} \end{array}\right]\dot{R}(t) \\ &=
\left[\begin{array}{ccc}\hat{X} & \hat{Y} & \hat{Z} \end{array}\right] \left[\omega_s\right]R\end{align}$$
즉, \(\left[\omega_s\right]R = \dot{R}\)이 되며 좌항의 \(R\)을 오른쪽으로 이항하여 다시 쓰면
$$\left[\omega_s\right] = \dot{R}R^{-1} = \dot{R}R^\text{T}$$
이라는 결과를 얻을 수 있다. 여기서 \(\omega_s\) 는 \(\vec{\omega}\) 를 fixed frame 에서 표현했다는걸 기억하자. 그러면 body frame 에서 표현한 \(\omega_b\) 는 \(R\) 과 어떤 관계일까?
\(\omega_s = R_{sb}\omega_b = R\omega_b\)
이므로 위 식에 넣으면
\(\left[\omega_s\right]=\left[R\omega_b\right]=R\left[\omega_b\right]R^\text{T} = \dot{R}R^\text{T}\)
이라는 관계식을 얻을 수 있다. 이를 정리하면
$$\left[\omega_b\right] = R^{-1}\dot{R} = R^\text{T}\dot{R}$$
임을 알 수 있다.